Algumas propriedades dos quadriláteros

Percentagens

Adquira agora o seu Atlas, escolhendo a modalidade que mais lhe interessar.

Resolução

Qual é a modalidade mais vantajosa para o vendedor?

Modalidade A: desconto de 40%
40% x 50 €=20 €

Resposta: A modalidade mais vantajosa para o vendedor é a modalidade B, pois ainda ganha 2€ ( desconto da modalidade A - a oferta da modalidade B, 20€-18€)

Divisão

Numa divisão inteira o quociente é 18, o divisor 11 e o resto 2. Qual é o dividendo?
Numa divisão inteira, 

Dividendo = divisor x quociente + resto

Dividendo = 11 x 18 + 2

Dividendo = 200

Média aritmética

A pontuação média de um teste feito a seis estudantes era de 84%. No entanto houve um erro, a pontuação de um estudante foi dada como 86%, quando na realidade a sua pontuação foi de 68%. Esse erro foi corrigido. Qual é a média corrigida?

84% x 6= 504%

504%- 86%= 418%

418%+68%=486%

486%:6= 81%

Resposta: A média corrigida é igual a 81%.

Problema

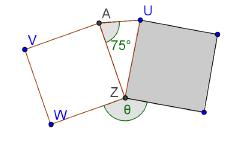
O quadrado cinzento é a imagem do quadrado [AVWZ], associada a uma rotação de centro em Z no sentido negativo.

Classifica o triângulo [ZUA] quanto aos lados e quanto aos ângulos.

O triângulo [ZUA] quanto ao comprimento dos lados é um triângulo isósceles ( dois lados iguais) e quanto à amplitude dos ângulos é um triângulo acutângulo.

Determina a amplitude da rotação (do quadrado) de centro em Z e sentido negativo.

Sabemos que O triângulo [ZUA] é isósceles (dois ângulos iguais cuja amplitude é 75º).
A amplitude do terceiro ângulo do triângulo é:
180º - (75º+75º)= 30º

Resposta: a amplitude da rotação do quadrado é igual a:
30º+90º= 120º
Determina a amplitude do ângulo q.

360º - (30º+2x90º)=

360º - 210º= 150º

Soma algébrica

Um gafanhoto está na posição 0 de uma reta numérica. Salta 5 unidades para a direita, em seguida 7 unidades para a esquerda, em seguida 5 unidades para a esquerda e finalmente 10 unidades para a direita. Qual é a posição atual do gafanhoto?

Resposta: 0 + (+5) + (-7) + ( -5 ) + (+10)= (+15) + ( -12)= +3

Problema: frações

Face do topo - 4 cubinhos
Face da frente - 6 cubinhos
Face de trás - 6 cubinhos
Face da esquerda - 6 cubinhos
Face da direita - 6 cubinhos
Total de cubinhos só com uma face coberta com chocolate= 4 + 4 x6 = 28 cubinhos

Todos os convidados comeram uma e apenas uma fatia de bolo, o João também comeu uma fatia. Sobraram 16 fatias. Um terço eram do género feminino. Quantos eram os rapazes?
Total de fatias= 64
Sobraram 16 fatias
64-16= 48 fatias que foram comidas pelos convidados e pelo João, portanto 48 pessoas ( pois cada uma comeu apenas uma fatia de bolo de chocolate).
1/3 x 48 = 16 pessoas do sexo feminino 
48 - 16 = 32 rapazes 
ou 2/3 x 48 = 32 rapazes

Ângulos internos e externos de um triângulo

Observa a figura.
O é o centro da circunferência. Qual é a amplitude do ângulo X?

Como sabes: 

O triângulo isósceles tem dois lados com o mesmo comprimento e dois ângulos com a mesma amplitude. ( 35º e 35º). 

A soma das amplitudes dos ângulos internos de um triângulo é 180º.

180º - (35º + 35º)= 180º - 70º= 110º

X é o ângulo externo do ângulo de 110º, a soma das suas amplitudes é 18oº.

180º - 110º = 70º   ou todo o ângulo externo de um triângulo é igual à soma das amplitudes dos outros dois ângulos internos não adjacentes ao mesmo: X = 35º + 35º = 70º

Problema: m.d.c

m.d.c (180, 300)= 2x2x3x5=60
Pela decomposição em fatores primos temos:
180= 2x2x3x3x5    300= 2x2x3x5x5
Resposta: O número máximo de embalagens que a Maria consegue fazer é igual a 60.

Qual é a composição de cada embalagem?
180 : 60 = 3 bombons de chocolate branco
300 : 60 = 5 bombons de chocolate preto

Resposta: Cada embalagem terá 3 bombons de chocolate branco e 5 bombons de chocolate preto

Considera o grafico, o qual representa as idades de um grupo de escuteiros.

Qual a variável em estudo? A idade dos escuteiros S. Cristovão.
Como a classificas? Variável quantitativa discreta.
Calcula a média.
Média= ( 5x10 + 10 x11 + 5 x 12):20
Média= 11

Qual é a moda e a amplitude? a moda é 11 (A moda é o valor que aparece mais vezes numa série de valores observados). A amplitude é a diferença entre o valor máximo e minino.

                                                         amplitude: 12 -10 =2 anos

Problema

Resposta: A altura da girafa é 4,14 metros.

problema

Num supermercado sempre que aparecem maças ou laranjas sensivelmente com 100 g de peso são selecionadas para embalagens de dois tipos. A embalagem do "tipo A" tem uma maça e uma laranja e custa 1,05€, a embalagem do "tipo B" tem duas maças e uma laranja e custa 1,65€.

Qual é a razão entre o preço de uma maça e de uma laranja? ( a razão compara duas grandezas).

preço da maça= 1,65 - 1,05 = 0,60€ 

preço da laranja= 1,05 - 0,60 = 0,45 €

0,60€= 60 cêntimos

0,45€= 45 cêntimos

60/45 = 12/9 = 4/3 ( quatro para três ).

O Sr. Jaime comprou 5 embalagens do "tipo A" e três do "tipo B". E possível que ele tenha pago a conta com moedas de 0,20 € sem receber troco? Se sim, quantas moedas foram necessárias?

5 x 1,05 + 3 x 1,65= 10,2 €

10,20 : 0,20 = 51

Resposta: Foram necessárias 51 moedas de 20 cêntimos.

Volume do cilindro

O Cilindro da figura tem um raio de 3 cm e uma altura de 10 cm. Calcula o volume do cilindro, arredondado às unidades por excesso.

raio= 3cm 

Vcilindro= 3,14 x raio x raio x altura

Vcilindro= 3,14 x 3cm x 3 cm x 10 cm=

Vcilindro= 282,6 cm3 = 283 cm3 (arredondado às unidades por excesso)
O João colocou uma fita à volta do cilindro (as extremidadedes da fita tocam-se), Qual é o comprimento em dm da fita para colocar à volta do cilindro?
O comprimento da fita é igual ao perímetro do círculo
Pcírculo= 3,14 x diâmetro
diâmetro = 2 x raio
diâmetro = 2 x 3 cm = 6 cm
P círculo= 3,14 x 6 cm = 18,84 cm =1,884 dm

Percentagens

Um automobilista foi multado em 75 euros e esqueceu-se de pagar a multa.  Foi obrigado a pagá-la, um mês depois, com 12% de juros. Quantou pagou?

Juros= 12% x 75 €= 9 €

multa + juros = 75€ + 9€= 84€

Resposta: Pagou 84€

Proporcionalidade direta

Observa o gráfico, relativo à quantia a pagar para percorrer uma certa distância, de camioneta. 

Trata-se de um gráfico de proporcionalidade directa? Justifica

Sim. Num gráfico de proporcionalidade directa todos os pontos estão sobre a mesma recta, que passa pela origem do referencial, ou seja, pelo ponto (0,0). 

Complete a tabela utilizando o gráfico. 

Qual a constante de proporcionalidade? O que representa? 

50:2 = 25, por cada 25 km percorridos de camioneta paga-se 1€.

Ângulos

Na figura: 

• Os pontos A, C e E pertencem à mesma reta. 

• Os pontos B, C e D pertencem à mesma reta. 

• O triângulo [ABC] é retângulo em A. 

• DÊC = 36º e CBA = 48º. 

Determina: 
A amplitude do ângulo ACB. Justifica a resposta.
A soma dos três ângulos internos de um triângulo é igual a 180º.
amplitude do ângulo ACB= 180º - (90º + 48º) = 42º
A amplitude do ângulo ECD. Justifica a resposta. 
Os ângulos ECD e ACB são ângulos verticalmente opostos, têm a mesma amplitude.
amplitude do ângulo ECD= 42º
A amplitude do ângulo CDE.
180º - (42º + 36º)= 102º

Problema: Áreas e Perímetros

A figura representa um semicírculo inscrito num retângulo. O perímetro do retângulo é 42 cm. A Joana afirmou que o raio do semicírculo é 7.  Explica como pode a Joana ter chegado a essa conclusão. 

Comprimento do retangulo= diâmetro do semicírculo

Altura do retângulo= raio do semicírculo

Diâmetro= metade do raio

Comprimento do retângulo= 2 x altura

Pretângulo= 2 x comprimento + 2 x altura

Pretângulo= 2 x (2 x altura) + 2 x altura

Assim, 42 cm : 6= 7 cm

comprimento= 14 cm e altura= 7 cm

Calcula a área da parte não colorida da figura.

Aretângulo= 14 cm x 7 cm= 98 cm2

Acírculo= 3,14 x raio x raio

Acírculo= 3,14 x 7 cm x 7 cm= 153,86 cm2

Área do semicírculo= 153,86 cm2 : 2 = 76,93 cm2

Área da parte não colorida= Aretângulo - Asemicírculo

Área da parte não colorida= 98 cm2 - 76,93 cm2

Área da parte não colorida= 21,07 cm2

máximo divisor comum

A Filipa tem 6 balões verdes, 12 azuis e 24 vermelhos e pretende fazer conjuntos de balões de modo que todos os conjuntos tenham o mesmo número de balões  de cada cor e não sobre nenhum. No máximo quantos conjuntos de balões podem fazer? 

Resolução:

m.d.c(6,12,24)= 2 x 3 = 6

6= 2 x 3

12= 2 x 2 x 3

24= 2 x 2 x 2 x 3

Serão feitos 6 conjuntos de balões. Cada conjunto será constituído por: 1 balão verde, 2 balões azuis e 4 balões vermelhos.

Perímetro de uma figura

Calcula o perímetro da seguinte figura:

Pcírculo= 3,14 x diâmetro
Pcírculo= 3,14 x 10 cm
Pcírculo= 31,4 cm
Psemicirculo= 31,4 cm :2= 15,7 cm
Perímetro da figura= 2 x 15,7 cm + 2 x 12 cm + 2 x 15 cm
Perímetro da figura= 85,4 cm

Números inteiros relativos

Considera os números escritos nos caracóis.

Escreve os números por ordem crescente?

-241 < -12 < -5 < -2 < 0 < +5 < +12 < +117

Indica dois números que sejam simétricos. (Números simétricos-  são dois números que estão à mesma distância da origem, isto é, têm o mesmo valor absoluto e sinais contrários).

Resposta: -12 e +12

Qual é o número maior? + 117

Qual é o número menor? -214

Qual é o número de maior valor absoluto? -241

Números inteiros relativos

Coloca por ordem crescente os números:

–13;  +20;  0;  –76;  +12;  –4;  +1;  –1

Resposta:

-76 < -13 < -4 < -1 < 0 < +1 < +12 < + 20

Problema: Volume do cilindo

O cilindro da figura tem 552,64 cm3 de volume. Determina a sua altura.

Vcilindo=3,14 x raio x raio x a

raio= diâmetro :2

raio= 8cm :2 = 4 cm

552,64 cm3= 3,14 x 4cm x 4cm x a

552,64 cm3= 50,24 cm2 x a

a= 552,64 cm3 : 50,24 cm2

a= 11 cm

Problema: Volume do Cilindro

O bidão de gasolina da figura está cheio até 75% da sua capacidade. Quantos litros de gasolina contém?

Vcilindro= 3,14 x 0,4m x 0,4 m x 1m=0,5024 m3=502,4 dm3= 502,4 l

75% x 502,4 l=376,8l

Resposta: Contém aproximadamente 377 litros de gasolina.

Problema: Volume do cilindro

Quantas garrafas de azeite é possível encher com o conteúdo do depósito?

Vdepósito=3,14 x 0,5 m x 0,5 m x 1,2 m=0,942 m3=942 dm3= 942l

nº de garrafas= 942l : 1,5l= 628

Resposta: É possível encher 628 garrafas de azeite

Recordar: Cilindro

Percentagens

Numa escola, o número total de alunos, professores e funcionários é 1600. O gráfico seguinte ilustra a situação:

Qual a percentagem correspondente aos funcionários?

100% - (85% + 10%)= 5%

Resposta: corresponde a 5% 

Determina o número de alunos, professores e funcionários desta escola.

professores: 10% x 1600 = 160

alunos= 85% x 1600 = 1360

funcionários = 5% x 1600 = 80

Problemas: Proporções

Num parque de campismo estão tendas e caravanas na razão 7 : 5, num total de 168.

Determina o número de tendas e de caravanas que estão no parque.
168 ( total de tendas e caravanas)

7/12 = nº de tendas/168

nº de tendas= (7 x 168 ):12

nº de tendas = 98 

nº de caravanas = 168 - 98 = 70

Recordar: Estatística

Recordar: Operações com números racionais

Problema: Perímetro do retângulo

Um jovem atleta dá passadas regulares de 70 cm.Quantas passadas terá de dar para contornar um jardim rectangular de 6 m de comprimento por 2,4 m de largura? 

Perímetro do retângulo= 2 x comprimento + 2 x largura
Perímetro do retângulo= 2 x 6m + 2 x 2,4m= 12 m + 4,8 m= 16,8 m
16,8 m= 1680 cm
nº de passadas= 1680 cm : 70cm= 24
Resposta: Serão necessárias 24 passadas.

Operações com potências

Calcula:

Resolução:

Para recordar:

Para multiplicar potências com a mesma base, mantém-se a base e somam-se os expoentes.

Para multiplicar potências com o mesmo expoente, mantém-se o expoente e multiplicam-se as bases.

Para dividir potências com a mesma base, diferente de zero, mantém-se a base e subtraem-se os expoentes.

Para dividir potências com o mesmo expoente, mantém-se o expoente e dividem-se as bases. (divisor diferente de zero)

Problema: Perímetro, Área e Volume

Observa a figura:

Um destes depósitos contém 220 000 litros de água. Qual é o depósito? 
VA=Abase x altura
Abase= 3,14 x 6m x 6m=113,04 m2
VA=113,04 m2 x 2m=226,08 m2= 226080 dm3= 226080 l
VB= 6 m x 8m x 4m= 192 m3 = 192000 dm3= 192 000 dm3
Resposta: O depósito A, pois o B só tem capacidade para 192000 l.

Pretende-se pintar a superfície lateral do depósito cilíndrico. Sabendo que se gastam 2 litros de tinta por cada metro quadrado, quantos litros de tinta serão necessários?

Superfície lateral do cilindro= retângulo

Pcírculo= comprimento do retângulo

Pcirculo=3,14 x 12m = 37,68m

Área do retangulo= 37,68m x 2m = 75,36m2

75,36m2:2=37,68l= 38l

Perímetro de uma figura

Calcula o perímetro da figura:

Perimetro do círculo= 3,14 x diâmetro
Perimetro do círculo= 3,14 x 4 cm = 12,56 cm
Perímetro da figura = 12,56 cm + 4 cm = 16,56 cm

Recordar: Equivalências

Medidas de Superfície - Servem para avaliar as extensões que  possuem  duas dimensões: comprimento e largura. 

Medidas agrárias-  Servem para avaliar as superfícies de campos,  sendo por  isso medidas agrárias que estão, entre si, na razão de 1 para 100. A principal unidade destas medidas é o are (a). Possui um múltiplo, o hectare (ha), e um submúltiplo, o centiare (ca). 

1 ha = 1hm²
1a = 1 dam²
1ca = 1m²

Recordar: Equivalências

Para recordar:O litro é uma unidade de medida de volume ou capacidade.

Cada litro corresponde a 1 decímetro cúbico

1l = 1dm3

Problema: Frações

Ao estudar para o teste de matemática, o José resolveu dois nonos dos exercícios que a professora indicou. A Sara resolveu cinco sextos desses exercícios e a Inês três quartos.

Quem resolveu mais exercícios?

1º Vamos calcular o m.m.c dos denominadores ( vamos reduzir ao mesmo denominador)

m.m.c(4,6,9)=36

36:4=9    36:6=6 ; 36:9=4

2º Aplicar a regra de equivalência de frações, ou seja,multiplicar os numeradores e os denominadores pelos quocientes anteriores ( 9, 6 e 4 ).

2/9=8/36  ; 5/6=30/36 ; 3/4=27/36

Resposta: Quem resolveu mais exercícios foi a Sara, pois 5/6 é maior do que 2/9 e 3/4.

Se  caderno de atividades tiver 54 exercícios, quantos resolveu cada um?

José - 2/9 x 54= 12 exercícios;

Sara - 5/6 x 54= 45 exercícios;

Inês - 3/4 x 54= 40 exercícios completos. (= 40,5)

Que percentagem de exercícios resolveu a Inês?

3/4 = 75/100= 0,75=75%

Experiências aleatórias

O Pedro tem um saco com 10 berlindes brancos, 6 berlindes pretos e um berlinde vermelho. Retirou um berlinde do saco. 

Indica : 

Um acontecimento impossível;  sair um berlinde verde

Um acontecimento pouco provável; sair um berlinde vermelho

O acontecimento mais provável; sair um berlinde branco 

É mais provável sair berlinde preto ou branco? Sair um berlinde branco. Porquê?

Porque em 17 berlindes, 10 são brancos e 6 pretos, ou seja, 10/17 > 6/17

Problema: Área

A área que envolve os lagos da tartaruga está vedada e tem 8 m de comprimento e 5 m de largura. Entre a vedação e o lago há uma zona verde com 1 m de largura onde os animais se podem deslocar.

Calcula a medida da área do lago.
comprimento= 8m - 2m = 6m       largura= 5m - 2m= 3m
Área= c x l
Área= 6m x 3m= 18m2

Calcula a medida da área de que as tartarugas dispõem para se deslocarem fora da água

Área total - Área do lago = 40m2 - 18m2= 22m2

Área total= 8m x 5m = 40 m2

Resposta: As tartarugas dispõem de 22 m2 de área para se deslocarem fora da água

Problema: Perímetro

O Diogo e o José gostam de andar de bicicleta. O Diogo andou de bicicleta à volta de uma pista formada por um retângulo com 15 metros de comprimento e dois semicírculos com 8 metros de diâmetro. Qual a distância percorrida pelo Diogo no fim de dar três voltas à pista?

Pcírculo= 3,14 x 8m = 25,12 m ( Psemicírculo= 25,12:2=12,56 m)
Distância percorrida numa volta= 25,12m + 2 x 15m=55,12m   (25,12m= 2x12,26m)
Distância percorrida em três voltas= 3 x 55,12= 165,36 m

Problema: Frações

Comprei um computador por 895 euros. Dei de entrada dois quintos do seu valor e o restante dividido em 12 prestações mensais iguais. Quanto devo pagar em cada prestação?

1º- Vamos calcular o valor da entrada

2/5 x 895= 358 euros
2º- Vamos calcular a quantia a ser paga em prestações
895€ - 358€=537€
3º- Calcular a prestação mensal a pagar 
537€:12= 44,75 €
Resposta: Deverá pagar 44,75 € por mês.

Estatística

Foi realizado um inquérito nas turmas de MACS do 10º ano da Escola Secundária Quinta das Flores com o objetivo de estudar determinadas características. Uma das características estudadas foi a idade dos alunos e os resultados obtidos encontram-se no seguinte gráfico: 

Qual é população em estudo?  Os alunos de MACS do 10º ano da Escola Secundária Quinta das Flores.

Qual a amostra em estudo? 33 alunos

Identifica a variável em estudo e classifica-a. A idade dos alunos. Varíável quantitativa e discreta.

Qual a percentagem de alunos com 18 anos? 2:33 x 100= 6%  

Qual a média de idades dos alunos de MACS? 

Temos que somar todas as idades e de seguida,  dividir o resultado pelo número de alunos inquiridos

(14 + 13 x15 + 14 x 16 + 3 x 17 + 2 x 18):33

520:33=15 anos ( 15,7575... )

Diagrama de caule-e-folhas

Na escola do Tobias, um grupo de alunos decidiu jogar ao pião. O jogo consistia em lançar o pião, colocá-lo na mão e contar o número de segundos que o pião permanecia a rodar na mão. O registo dos tempos, em segundos, foi organizado no seguinte diagrama de caule-e-folhas:

Com base no diagrama de caule-e-folhas responde:

Quantos alunos participaram no jogo do pião? Participaram no jogo 25 alunos.

Quanto permaneceu o pião a rodar na mão do aluno que ganhou o jogo? O aluno que ganhou o jogo manteve o pião a rodar na mão 45 segundos.

Os alunos que mantiveram o pião a rodar na mão mais de 30 segundos ficaram apurados para o campeonato do pião. Quantos alunos foram aputados? 8 alunos foram apurados para o campeonato do pião.

Qual a percentagem de alunos que manteve o pião a rodar na mão mais de 40 segundos?

2 : 25 x 100= 8%  (25/100 = 2/x  ;   x= 2 x 100 : 25)

Qual é a moda?17 segundos.